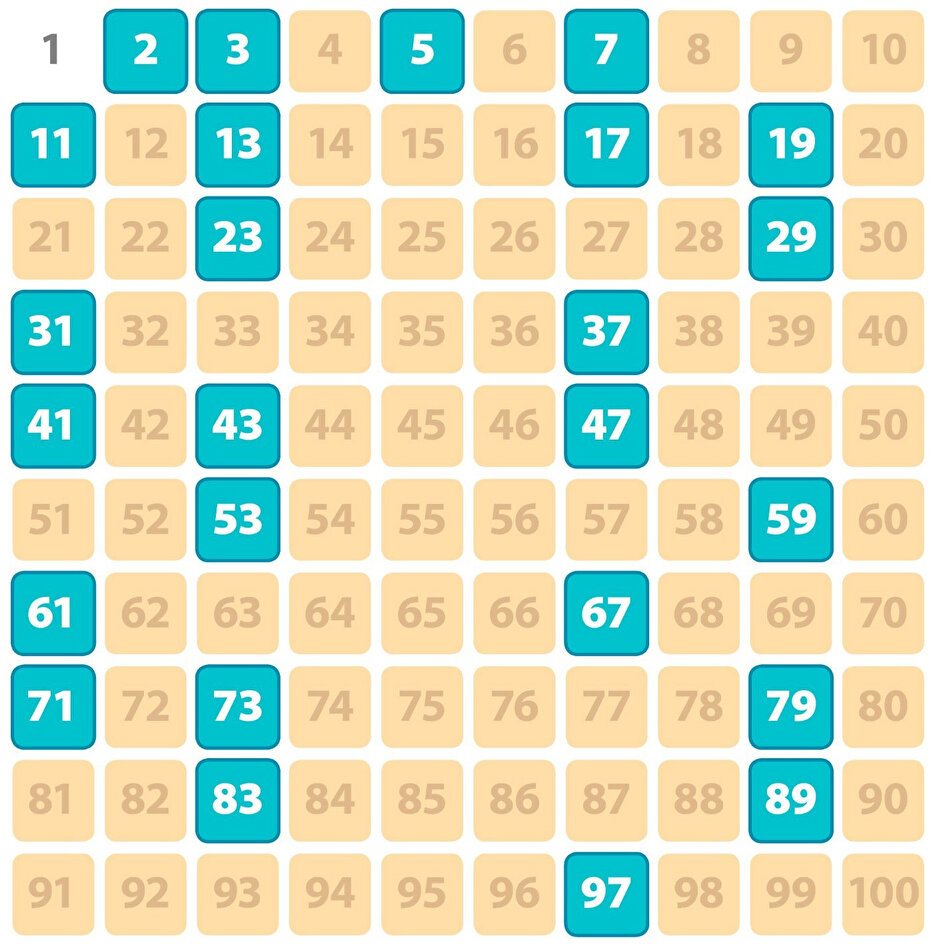
İki pozitif tam sayı böleni olan doğal sayılar olarak bilinen asal sayılar, sadece kendisine ve 1 sayısına kalansız bölünebilen tam sayılardır. Matematikte sıkça karşılaşılan ve önemli bir konu olan asal sayılar, matematiğin temel işlemlerini yapabilmekte önemli bir rol oynar. İnsanlar asal sayının nasıl bulunacağı konusunda araştırmalarda bulunuyor. Peki asal sayılar nelerdir? İkiz asallar nelerdir? Asal çarpan ve aralarında asal sayı nedir? Asal sayılar sonsuz mudur? Asal sayılar nasıl bulunur? İşte tüm soruların cevapları ve 1'den 100'e kadar asal sayı tablosu.
Matematikte en çok karşılaşılan konulardan asal sayılar, çoğu insanın araştırdığı bir konu. Asal sayılar ve özellikleri ilk olarak antik Yunan matematikçileri tarafından incelenmiştir. Asal sayılar hakkındaki pek çok soru günümüzde hala cevaplanamamaktadır.
ASAL SAYILAR NELERDİR, HANGİLERİDİR?
1 sayısı asal bir sayı sınıfına girmez. Asal sayılar 2'den başlamaktadır. 2 en küçük asal sayıdır. 2 haricinde bütün asal sayılar tek sayılardır. Çift sayıların tamamı 2 ile kalansız bir şekilde bölünür.
Bu nedenle de 2'den büyük olan çift sayıların hepsinin en az 3 adet çarpanı bulunur. Bu sebeple de 2 dışındaki çift sayılar asal sayı kategorisine giremez.
ASAL SAYILAR NASIL BULUNUR?
- Sadece kendisine ve1'e bölünebilen 1'den büyük doğal sayılar asal sayıdır.Karşılaşılan sayının kendisi dışında bir böleni bulunmuyor ise o bir asal sayıdır.Asal sayılar bu şekilde bulunabilir.Bir (1) tanım gereği asal sayı değildir.
İKİZ ASALLAR NELER?
Aralarındaki fark iki olan asal sayılar ikiz asallardır.
> (3, 5)
> (5, 7)
> (11, 13)
> (17, 19)
> (29, 31)
> (41, 43)
> (59, 61)
> (71, 73)
> (101, 103)
> (107, 109)
ASAL ÇARPAN NEDİR?
Bir sayının çarpımlarından asal olanlarına “asal çarpan” denir. 1’den büyük her tam sayı aslında ya asal bir sayıdır ya da asal sayıların çarpımlarından oluşur.
Örneğin 11 asal bir sayı iken, 12 sayısı 12=22.3 şeklinde asal sayıların çarpımı sonucu elde edilir.
Aynı şekilde 21 sayısı 21=3.7 şeklinde yazılabilir. Yani 1’den büyük her tam sayı asal sayılar ile üretilir.
ARALARINDA ASAL SAYI NEDİR?
1’den başka ortak böleni bulunmayan iki pozitif tam sayıya “aralarında asal sayı” denir.
Örneğin 9 ve 10 sayılarının EBOB’u 1’e, EKOK’u ise 90’a eşittir. Görüldüğü gibi aralarında asal sayıların asal olma zorunluluğu yoktur. Asal iki sayı her zaman aralarında asaldır.
- Ayrıca asal sayılar şifrelemede kullanılır. Örneğin günümüzde kullandığımız e-posta ve diğer tüm dijital işlemlerde veriler RSA şifreleme yöntemiyle şifrelenir. RSA şifreleme yönteminde olabildiğince büyük asal sayılar kullanılır. Böylece istenmeyen kişilerin verilere ulaşması engellenir.
ASAL SAYILAR SONSUZ MUDUR?
Asal sayılar sonsuzdur. Asal sayıların sonsuzluğunun ilk ispatını Öklid isimli İskenderiyeli matematikçi vermiştir.
ASAL SAYILARI KİM BULDU?
Asal sayılar ve özellikleri ilk olarak antik Yunan matematikçileri tarafından incelendi. Pisagor okulunun matematikçileri, MÖ 500-MÖ 300 yılları arasında mükemmel sayılar gibi gizemli özellikleri olan sayılarla ilgileniyorlardı. Bu sırada asal sayıların da özelliklerini anladılar ve bu sayılar üzerinde ayrıntılı çalışmalar yaptılar.
